Marketers today have more control over their advertising investment than ever before. By control, I mean marketers have many options for how to spend their ad dollars, very little commitment in terms of minimum spend levels, and rich data to pour through to measure results. Marketers can reallocate their ad budget weekly, daily, even hourly for certain channels. Despite this flexibility, however, many marketers still use antiquated methods to optimize their ad budgets. Here are six tips to help you systematically boost your marketing performance.
Fractional Factorial Experimental Design
Hypothesis testing has always been a cornerstone of marketing optimization. When you have addressable audiences and you’re conducting a simple experiment, a simple randomly split A/B test will work. But what if you want to conduct several experiments simultaneously?
Fractional factorial experimental design is a great way to screen main effects and conduct several tests simultaneously, providing a statistically significant way to read which effects deserve additional testing. All while spending a fraction of the ad budget required for a full factorial test.
Let’s say you want to test 4 factors in a multi-channel test, and each factor has two levels (on or off). For example, you may want to construct a prospecting test to an addressable audience using a combination of direct mail, email, Facebook and online display ads. We’d like to know how much lift each channel provides in generating new customers, with the ability to read interactions between the tactics as well. A full factorial two-way test with four factors would require 2^4 experiments, or 16 cells. A fractional factorial design of resolution four (IV) would allow you to conduct the test with half the cells.
The table below illustrates the 16 cells required for a full factorial test, and the shaded cells required for a fractional factorial test with resolution IV. In this example, 0 implies ‘off’ and 1 implies ‘on’.
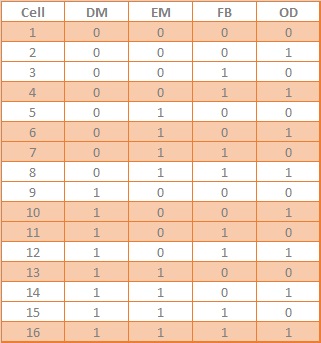
Fractional factorial design specifications follow the syntax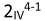 
with k representing the number of factors to be tested, p representing the number of those factors generated from the interactions of a full factorial set, and res indicating the test resolution.
The design above is described as a .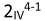
Fractional factorial designs will sacrifice your ability to read certain interactions among the factors in your test. The level of sacrifice is indicated by the resolution. Only a full factorial test will provide full resolution.
Generally, a design of resolution (R) is not confounded with any other interaction (I) of an order less than R-I. In our resolution four (IV) test, 1 way interactions (I=1) are not confounded with any interactions less than 4-1 = 3-way interactions. Meaning, no main effects (1-factor interactions) are confounded with any other main effects or two-factor interactions, but they’re confounded with three-factor interactions. For example, you can interpret the effects of two variables combined (e.g. email + Facebook, direct mail + display ads), but not three-factor interactions (email + Facebook + display ads). If multiple-interaction effects are considered to be negligible, you can use a lower resolution test (but not below resolution III).
Back to our test design above, an ‘on’ strategy for any given channel does not need to imply one impression, but rather a specific strategy. For example, 1 for e-mail could imply 2 emails, 1 for Facebook could imply 8 newsfeed ads over a three-week duration with daily caps, and 1 for online display could imply 20 impressions over a three week period with daily caps.
Generally speaking, designs of resolution three or four are designed to screen out the few important main effects from the many less important factors. Keep in mind that as you increase the resolution of a test in order to read interaction effects, you will be required to introduce more experiments (test cells), and defeat the purpose of a fractional factorial test (to test more effects with less ad dollars). Here’s a useful link for a table of common fractional factorial designs.
Recent Comments